Пересечения

Пересечения

Это тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Метод Эйлера является незаменимым при решении таких задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

Иностранные языки

В туристической группе было 24 человека. Шесть из них не знали ни одного иностранного языка. Из остальных тринадцать знали английский язык. Четыре туриста, которые знали английский, могли говорить и по-немецки.

Сколько туристов знали только немецкий?

Решение

Задача достаточно проста, ее можно решить арифметически.

(24 – 6) – 13 = 5

Ответ. 5 туристов знали только немецкий язык.

Любимые мультфильмы

Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок».

Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма.

Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма.

Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

Решение.

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

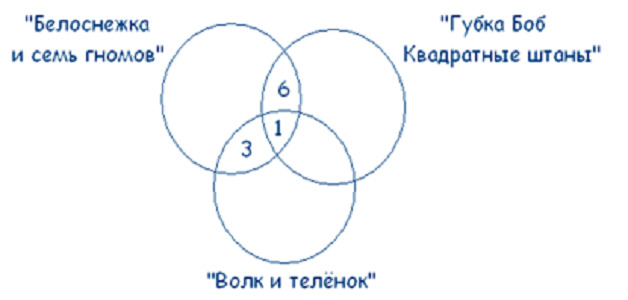
Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

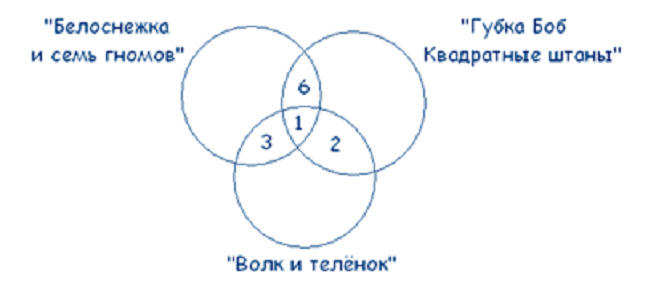
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Получаем:

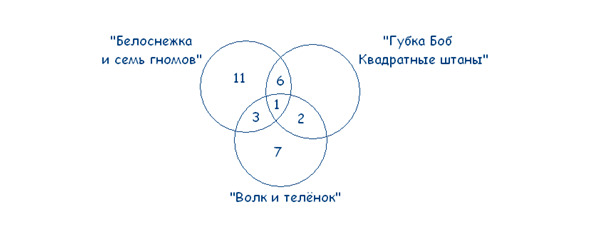
38– (11 +3 +1 +6 +2 +7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны». Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 +2 +1 +6 = 17 человек.

Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

Задачи для тренировки

1. Волшебные книги

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

2. Пионерский лагерь

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

3. Экстрим

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

4. Помогите разобраться

В классе 15 человек говорят по-английски, 20 – по-итальянски, 8 – по-немецки; 3 – по-немецки и по-английски; 5 – по-немецки и по-итальянски; 6 – по-итальянски и по-английски. Сколько человек в классе, если всеми тремя языками владеет 1 человек?

Данный текст является ознакомительным фрагментом.