Логика
Логика
Многие проблемы в общении возникают от того, что люди не знают основных законов логики.
По определению из словаря, логика – это искусство рассуждения, наука о способах доказательств и опровержений. Как наука она изучает способы достижения истины в процессе познания не благодаря чувственному опыту, а с помощью знаний, полученных ранее. Поэтому ее также можно определить как науку о принципах получения выводного знания.
В царской России логика была обязательным предметом в школе. Считалось, что каждый интеллигентный человек должен знать ее основы.
Сейчас для многих это слово нарицательное, модное, не несущее в себе никаких законов.
Те, кто уже изучил логику и используют теорию на практике, с легкостью замечают обрыв логической цепочки или подмену в речах крупных политиков, сразу видят, в чем подвох какой-либо программы.
Я не буду углубляться в теорию логики, вы без труда найдете книги в любом книжном магазине, например учебники Гетмановой или Челпанова, расскажу лишь о нескольких аспектах, которые мне очень близки. Сначала познакомьтесь с понятиями, основанными на законах логики, которые можно встретить и в технике нейролингвистического программирования.
Номинализации – это такие искажения, в результате которых непрерывные процессы представляются как законченные. (У нас плохие отношения. Твое поведение неприемлемо. Ты плохо ко мне относишься.)
Чтение мыслей – знакомый вид искажений. (Я знаю, все против меня. Я знаю, что ты сейчас чувствуешь.)
Причинно-следственная связь – ситуация, когда человек выставляет другого ответственным за нечто, к чему тот не имеет ни малейшего отношения. (Ты меня бесишь/ пугаешь. Ты имеешь надо мной власть.) Нужно задать вопросы: Как именно я тебя бешу/пугаю? Какую власть над тобой имею?
Замените вопрос «Почему?» более конструктивным «Зачем?»! «Почему ты продал свой дом?» Чувствуется безысходная грусть. Сравните: «Зачем ты продал дом?» Тут есть интерес, вероятность новых возможностей, выяснение, какова цель. Возникает другой эффект, чем от «Почему ты это сделал» (такой вопрос более походит на риторический).
А теперь – классическая основа логики в сокращенном варианте. Я знаю, что сначала теория покажется скучной и сложной. Но при более детальном изучении обязательно увлечет вас.
Индукция (от лат. induction – наведение) – процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго, а, скорее через некоторые фактические, психологические или математические представления. Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.
Объективным основанием индуктивного умозаключения является всеобщая связь явлений в природе.
Примерами индукции могут служить рассуждения:
Аргентина является республикой; Бразилия – республика; Венесуэла – республика; Эквадор – республика.
Аргентина, Бразилия, Венесуэла, Эквадор – латиноамериканские государства.
Все латиноамериканские государства являются республиками.
Различают полную индукцию – метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности, и неполную индукцию – при этом наблюдения за отдельными частными случаями наводят на гипотезу, которая, конечно, нуждается в доказательстве. («Наполеон – полководец; Суворов – полководец; значит, каждый человек полководец».)
Также для доказательства используется дедукция.
Дедукция (от лат. deductio – выведение) – метод мышления, при котором частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозаключений (рассуждений), звенья которой (высказывания) связаны отношением логического следования.
Метод дедукции прославил Шерлок Холмс.
К примеру, в Риме Конан Дойл берет извозчика, и тот говорит: «А, господин Дойл, приветствую вас после вашего путешествия в Константинополь и Милан!» «Как мог ты узнать, откуда я приехал?» – удивился такой шерлок-холмсовской проницательности Конан Дойл. «По наклейкам на вашем чемодане», – хитро улыбнулся кучер.
Началом (посылками) дедукции являются аксиомы, постулаты или просто гипотезы, имеющие характер общих утверждений (общее), а концом – следствия из посылок (частное). Если посылки дедукции истинны, то верны и ее следствия. Дедукция – основное средство доказательства.
Пример дедуктивного умозаключения:
Все люди смертны.
Сократ – человек.
Следовательно, Сократ смертен.
Если идет дождь, земля является мокрой.
Идет дождь.
Земля мокрая.
Простой категорический силлогизм – рассуждение мысли, состоящее из трех простых высказываний: двух посылок и одного заключения. Посылки силлогизма разделяются на большую (содержит предикат заключения) и меньшую (содержит субъект заключения). По положению среднего термина (см. ниже) силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения – на модусы.
Пример силлогизма:
1. Всякий человек смертен (большая посылка).
2. Сократ – человек (меньшая посылка).
–
3. Сократ смертен (заключение).
Рассмотрим структуру простого категорического силлогизма.
В отличие от терминов суждений – субъекта (S) и предиката (P) – понятия, входящие в состав силлогизма, называются терминами.
Различают меньший, больший и средний термины:
• S – меньший термин: субъект заключения (входит также в меньшую посылку);
• P – больший термин: предикат заключения (входит также в большую посылку);
• M – средний термин: входит в обе посылки, но не входит в заключение.
Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: большую – на первом месте, меньшую – на втором. Под чертой записывают заключение. Однако в практике рассуждения такой порядок необязателен.
Подлежащие S (субъект) – то, относительно чего мы высказываем (делится на два вида суждений):
1. Определенное: единичное, частное, множественное.
• Единичные – те, в которых подлежащее является индивидуальным понятием. Пример: «Ньютон открыл закон тяготения».
• Частные – те, в котором подлежащим суждения является понятие, взятое в части своего объема. Пример: «Некоторые S суть P».
• Множественные – те, в которых несколько подлежащих классовых понятий. Пример: «насекомые, пауки, раки есть членистоногие».
2. Неопределенное. Пример: «Светает», «Больно» и т. п.
Сказуемое P (предикат) – то, что мы высказываем (делится на два вида суждений):
• Повествовательные – это суждения относительно скоропроходящих событий, состояний, процессов или деятельности. Пример: «Роза в саду цветет».
• Описательные – суждения, в которых одному или многим предметам приписывается какое-нибудь свойство. Субъектом всегда является нечто определенное. Пример: «Огонь горяч», «Снег бел».
Между подлежащим и сказуемым могут быть:
• Тождество – понятия субъекта и предиката имеют один и тот же объем. Пример: «Всякий равносторонний треугольник есть равноугольный треугольник».
• Подчинение – понятия с менее широким объемом подчиняется понятию с более широким. Пример: «Собака есть домашнее животное».
• Отношение – именно пространства, времени. Пример: «Дом находится на улице».
При определении отношения между подлежащим и сказуемым важна четкая формализация терминов. Бездом ная собака хоть и не является домашней, поскольку не проживает в доме, все равно относится к классу домашних животных. То есть следует понимать, что домашнее по социально-биологической классификации животное в отдельных случаях может быть не домашним по месту обитания, то есть с социально-бытовой точки зрения.
Рассмотрим классификацию простых атрибутивных высказываний по качеству и количеству.
По качеству и количеству различают четыре вида простых высказываний:
• A – общие («Все люди смертны»).
• I – частноутвердительные («Некоторые люди – студенты»).
• E – общеотрицательные («Ни один из китов не рыба»).
• О – частноотрицательные («Некоторые люди не являются студентами»).
Примечание. Для условного буквенного обозначения высказываний используются гласные из латинских слов affirmo (я утверждаю, говорю «да») и nego (я отрицаю, говорю «нет»).
Распределенность терминов в простых высказываниях:
1. Субъект всегда распределен в общем высказывании и никогда не распределен в частном высказывании.
2. Предикат всегда распределен в отрицательных суждениях, в утвердительных он распределен тогда, когда по объему Р<=S.
В качестве предиката в некоторых случаях может выступать субъект.
Правила простого категорического силлогизма:
Средний термин должен быть распределен хотя бы в одной из посылок.
Термин, не распределенный в посылке, не должен быть распределен в заключении.
Число отрицательных посылок должно быть равно числу отрицательных заключений.
В каждом силлогизме должно быть только три термина.
А теперь поговорим о фигурах и модусах.
Фигурами называются формы силлогизма, отличающиеся расположением среднего термина в посылках:

Каждой фигуре отвечают модусы – формы силлогизма, различающиеся количеством и качеством посылок и заключения. Модусы изучались еще средневековыми школами, и для правильных модусов каждой фигуры были придуманы мнемонические имена:

Обращайте внимание на гласные в этих словах. A, I, E, O – по типам простых высказываний. И возможные комбинации с ними.
Следующие примеры силлогизмов каждого типа взяты из книги А. А. Ивина «Современная логика».
Barbara
Все животные смертны.
Все люди – животные.
Все люди смертны.
Celarent
Ни одна рептилия не имеет меха.
Все змеи – рептилии.
Ни одна змея не имеет меха.
Darii
Все котята игривые.
Некоторые домашние животные – котята.
Некоторые домашние животные – игривые.
Ferio
Ни одна домашняя работа не весела.
Некоторое чтение – домашняя работа.
Некоторое чтение не весело.
Cesare
Ни одна здоровая еда не полнит.
Все торты полнят.
Ни один торт не здоровая еда.
Camestres
Все лошади имеют вздутие живота.
Ни один человек не имеет вздутия живота.
Ни один человек не лошадь.
Festino
Ни один ленивый человек не сдает экзамены.
Некоторые студенты сдают экзамены.
Некоторые студенты не ленивы.
Baroco
Все информативные вещи полезны.
Некоторые сайты не полезны.
Некоторые сайты не информативны.
Darapti
Все фрукты питательны.
Все фрукты вкусны.
Некоторые вкусные продукты питательны.
Disamis
Некоторые кружки красивы.
Все кружки полезны.
Некоторые полезные вещи красивы.
Datisi
Все прилежные мальчики в этой школе рыжие.
Некоторые прилежные мальчики в этой школе – пансионеры.
Некоторые пансионеры в этой школе рыжие.
Felapton
Ни один кувшин в этом шкафу не нов.
Все кувшины в этом шкафу треснутые.
Некоторые треснутые вещи в этом шкафу не новы.
Bocardo
Некоторые кошки бесхвосты.
Все кошки – млекопитающие.
Некоторые млекопитающие бесхвосты.
Ferison
Ни одно дерево не съедобно.
Некоторые деревья зеленые.
Некоторые зеленые вещи не съедобны.
Bramantip
Все яблоки в моем саду полезны.
Все полезные фрукты зрелы.
Некоторые зрелые фрукты – яблоки в моем саду.
Camenes
Все яркие цветы ароматны.
Ни один ароматный цветок не выращен в помещении.
Ни один выращенный в помещении цветок не ярок.
Dimaris
Некоторые небольшие птицы питаются медом.
Все питающиеся медом птицы цветные.
Некоторые цветные птицы небольшие.
Fesapo
Ни один человек не совершенен.
Все совершенные существа мифические.
Некоторые мифические существа не люди.
Fresison
Ни один компетентный человек не ошибается.
Некоторые ошибающиеся люди работают здесь.
Некоторые работающие здесь люди некомпетентны.
В соответствии с правилами одни формы могут быть преобразованы в другие и все формы могут быть преобразованы в одну из форм первой фигуры.
Логический квадрат (идея принадлежит византийцу Михаилу Пселлу):
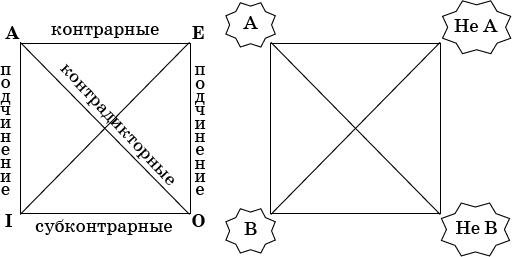
А – общеутвердительное
Е – общеотрицательное
I – частноутвердительное
О – частноотрицательное
Логический квадрат схематически показывает взаимодействие простых высказываний в последовательной речи. Он позволяет с легкостью обнаружить ошибки обобщения, противоречие.
И, наконец, мы подошли к основным логическим законам, понимание которых даст вам преимущество в любом общении: законам тождества, непротиворечия, исключенного третьего и достаточного основания.
«Закон тождества формулируется следующим образом: всякая мысль тождественна самой себе, то есть «А есть А», где А – любая мысль. При нарушении этого закона возможны следующие ошибки.
Амфиболия (от греч. amphibolos – двусмысленность, двойственность) – логическая ошибка, в основе которой лежит двусмысленность языковых выражений.
Пример: «Правильно говорят, что язык до Киева доведет. А я купил вчера копченый язык. Теперь смело могу идти в Киев». Другое название этой ошибки – «подмена тезиса».
Эквивокация – логическая ошибка при рассуждении, в основе которой лежит использование одного и того же слова в разных значениях.
Пример: «Старый морской волк – это действительно волк. Все волки живут в лесу. Таким образом, морские волки живут в лесу».
Здесь ошибка обусловлена тем, что в первом суждении слово «волк» используется в качестве метафоры, а во второй посылке – в прямом значении.
В логике этот прием еще называют «подменой понятия».
Логомахия – спор о словах, когда в процессе дискуссии участники не могут прийти к единой точке зрения в силу того, что не уточнили исходные понятия. То есть каждый вкладывал свой смысл в исходное понятие.
Таким образом, закон тождества выражает одно из важнейших требований логического мышления – определенность. Его нарушение также лежит в основе многих известных нам с детства задач и головоломок. Например, мы спрашиваем собеседника: «За чем (зачем) находится вода в стеклянном стакане?» – преднамеренно создавая двусмысленность в этом вопросе (зачем – для чего и за чем – за каким предметом, где). Собеседник отвечает на один вопрос, например он говорит: «Чтобы пить, поливать цветы», а мы подразумеваем другой вопрос и, соответственно, другой ответ: «За стеклом».
Закон непротиворечия гласит: два суждения, из которых в одном утверждается нечто о предмете мысли («А есть В»), а в другом то же самое отрицается об этом же предмете мысли («А не есть В»), не могут быть одновременно истинными.
Например, суждения «Данная река – приток Волги» и «Данная река не является притоком Волги» не могут быть одновременно истинными, если относятся к одной и той же реке.
Закон непротиворечия указывает на то, что из двух противоположных суждений одно необходимо ложно. Оно не может быть как истинным, так и ложным одновременно.
Закон исключенного третьего формулируется следующим образом: два противоречащих суждения не могут быть одновременно ложными: одно из них необходимо истинно; другое – необходимо ложно; третье суждение исключено.
Нельзя уклоняться от признания истинным одного из двух противоречащих друг другу высказываний и искать нечто третье между ними. Если одно из них признано истинным, то другое необходимо признать ложным и не искать третье.
Закон достаточного основания: для того чтобы считаться вполне достоверным, всякое положение должно быть доказано, то есть должны быть известны достаточные основания, в силу которых оно считается истинным. В науке достаточными основаниями считаются: а) положения об удостоверенных фактах действительности, б) научные определения, в) ранее доказанные научные положения, г) аксиомы, а также д) личный опыт».
Этот материал я взяла с сайта (http://nastya-logika.narod.ru/Zakony_logiki.html). Мне понравилось, как простым языком авторы донесли основные законы.
Знание логики и понимание ее основных законов очень упростит вам коммуникации. Вы будете мгновенно определять подмену понятий, для вас важно будет сразу определить исходные критерии.
Вы станете видеть разницу между логической цепочкой убеждений и ложной, нелогичной системой аргументации. Ведь высказывание либо верное, либо ложное, и третьего не дано.
Вы не будете отрицать все, как самодур, и посылать подчиненных искать то, чего нет и быть не может.
И вы будете верить только доказанным данным, привыкнете проверять достоверность источника, прежде чем делать выводы.
Владение логическими понятиями – это высший пилотаж, тяжелая артиллерия высокоразвитого человека. Оно значительно экономит время, так как не нужно часами выслушивать доводы, их содержание становится ясным довольно быстро.
И в выступлениях красноречивых политиков вы сразу будете видеть ложные логические цепочки (когда выводы ошибочны и не являются следствием сказанного ранее).
Изучайте логику, если хотите стоять на ступеньку выше и видеть чуть больше большинства.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Лошадиная логика
Лошадиная логика Однажды к ребе Меиру из Перемышля пришёл за советом мужчина. Он с горечью пожаловался, что в городе у него появился конкурент, который может пустить его по миру.– Обращал ли ты когда-нибудь внимание на то, что конь, подходя к водопою, бьёт копытом по
Глава 1 Логика потребителя
Глава 1 Логика потребителя 1.1. Розничный бизнес сегодня Сфера ритейла является одной из самых динамично развивающихся. Появляются новые розничные сети, уходят старые. При этом количество удобных площадок не увеличивается пропорционально аппетитам розничных сетей.
1.5. Логика потребления
1.5. Логика потребления Что же вообще покупает потребитель? Очевидно, что во всех случаях, в том числе и при посещении конкретной торговой точки, он покупает те товары/услуги, которые дают ему возможность решить свои проблемы, реализовать свои базовые мотивы. Набор базовых
«Сыщик», «логика», «дедукция»
«Сыщик», «логика», «дедукция» Почти 130 лет назад на свет появился Шерлок Холмс. Очаровательный и невыносимый, хитрый и честный, равнодушный и вспыльчивый – в каждую минуту он мог быть разным. Только одно его качество всегда оставалось постоянным – умный. Его имя стало
Логика (T)
Логика (T) Говорил ли вам когда-нибудь учитель литературы, что нужно вкладывать душу в работу и ясно выражать свои эмоции? Но вам казалось, что тогда сочинение получится каким-то неестественным, правда? Возможно, все потому, что креативность логиков проистекает из их
Логика игры
Логика игры Менеджер отеля научился играть в игру своего начальника, потому что ему понравилась эта игра.Игра имела следующую логику:Большинство людей сегодня не получают того, чего они хотят. Не получают желаемого от работы, не получают от семьи, от религии, от
Логика
Логика Многие проблемы в общении возникают от того, что люди не знают основных законов логики.По определению из словаря, логика – это искусство рассуждения, наука о способах доказательств и опровержений. Как наука она изучает способы достижения истины в процессе